Built with Processing
説明: 直線運動するボールが円柱の柱にぶつかって跳ね返る計算式を求めるテストです。
ぶつかったボールはその位置での円の法線(中心と円周上の点を結ぶ線)に対して、入射角=反射角となる方向に反射します。
|
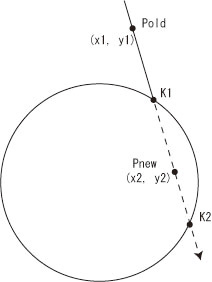
1)まず、円と直線の交点を求めます。 線分の両端の座標をPold(x1,y1)、Pnew(x2,y2)、交点をK(x,y)とすると、直線の方程式から、
y = ax + b
円の方程式から、 円と直線は、交わらないか、1点で接するか、2点で交わるかのいずれかですが、 交わる場合は、①②より、交点K1、K2が求まります。そのうち、開始点Poldに近いほうを交点Kとします。 直線がX軸に平行な場合とY軸に平行な場合は特殊な場合なので注意を要します。
|
|
|
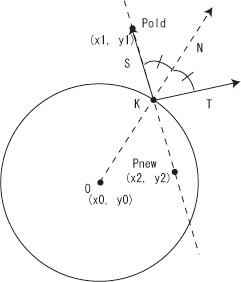
2)円での反射の方向を求めます。 交点KからPoldへ向かうベクトル S、円の中心から交点に向かう円の法線ベクトル N、交点Kから反射方向に向かう ベクトル Tを考えます。すべて単位ベクトルとします。
適当な計数 c,dを考えて、
入射角 = 反射角より、
③、④、⑤より、
これより、Tが求まるので、反射後の位置は次の位置Pnewに変更されます。vは適当な速度計数とします。 |
|